딥러닝의 기초 개념에서 거론되는 것 중 하나가 바로 XOR 문제인데요.
AND, OR 등은 Single Linear Separable 특성을 지니지만, XOR 문제에서는 조금 까다로워지기 시작합니다.
먼저 AND 함수를 가지고 살펴보면 다음과 같습니다.
[AND 함수 분류]
먼저 하나의 퍼셉트론을 가지고 분류를 하게되면,

출력 S(y) = W1*X1 + W2*X2 + W0
활성화 함수의 Decision Boundary가 0을 경계로 변경되기 때문에, y=0으로 설정하게 되면

위와 같이 수식을 정리할 수 있습니다.
이걸 X1, X2 평면에 표시하게 되면, 다음과 같습니다.



이때 기울기는 "-W1 / W2" 가 되고, 절편(Intercept)는 "-W0 / W2"가 되게 됩니다.
AND 와 OR, NOR 함수도 모두 동일하게 표현이 가능합니다.
그러나 XOR 함수는 얘기가 좀 달라지는데요.

먼저 AND, OR, XOR 함수를 평면에 그린 후 분류를 하게 되면 다음과 같이 표현이 가능합니다.
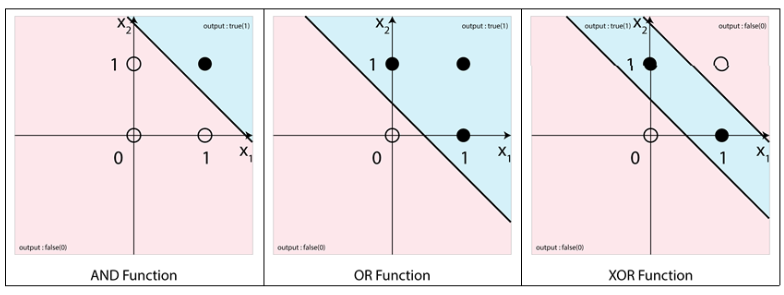
AND와 OR 함수의 경우에는 하나의 직선(Linear)으로 분류가 가능하지만, XOR 함수의 경우에는 두개의 직선(Linear)을 사용해야 합니다.
XOR의 문제는 1969년에 Marvin Minsky수와 Seymour Paper가 “Perceptrons: an introduction to computational geometry”라는 책을 통해 퍼셉트론의 한계를 수학적으로 증명한 사례입니다.
XOR Gate Problem
XOR은 최소 두개의 직선을 사용하거나 곡선을 이용해서 분류를 해야합니다.
이를 해결하기 위해 하나의 퍼셉트론을 추가하여 두개의 평면을 그리는 방법으로 접근을 하게 됩니다.

두개의 퍼셉트론을 적용하고 게이트 문제를 풀게되면 다음과 같이 풀이가 가능합니다.

(X1 AND X2)' 은 NAND 함수가 되기 때문에, OR 함수와 NAND 함수 그리고 AND 함수를 이용하여 표현할 수 있게 됩니다.

네트워크는 위와 같이 표현할 수 있게되고, 첫번째 Layer에 각각의 퍼셉트론에 OR와 NAND 게이트를 적용하고, 마지막 레이어에서는 AND 함수를 조합하게 됩니다. (마지막 레이어는 활성화 함수)

OR 함수를 거치는 Y1과 NAND 함수를 거치는 Y2를 테이블로 표현하면,

위와 같이 정리할 수 있게되는데, 이걸 평면으로 표현해보면 다음과 같습니다.

Y1, Y2는 기존 4 Point에서 3 Point로 줄었고, Linearly Spearable 상태가 됩니다.
이렇게 포인트의 수를 줄이는 방식으로 non-separable problem을 해결할 수 있습니다.
Increase the Dimmension
두번째 방법은 차원을 증가시키는 방법입니다.

기존에 우리가 하나의 직선으로 풀 수 없는 유형의 문제를 3차원으로 가져오게 되면 다음과 같이 표현이 가능합니다.
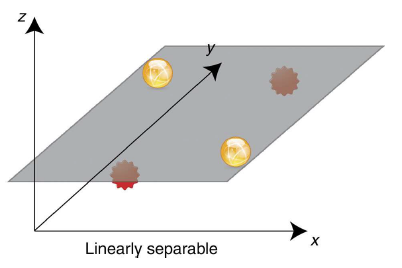
3차원 공간의 Depth가 생기게 되면서, 하나의 3차원 평면으로 분류를 할 수 있게 되는 것이죠.


중간 퍼셉트로에 x1과 x2의 AND 조건으로 만들어주고, 넣어줌으로 3차원 좌표를 만들 수 있습니다.




