경사하강법은 가중치를 업데이트 하면서 예측값과 실제값간의 차이를 줄여주기 위한 방법입니다.
앞선 포스팅에서 Adaline에 대해서 설명했는데, Adaline에서 손실함수를 사용하여 최적의 가중치를 찾게 되는데요.
손실함수 MSE 는 2차함수로 표현이 되고, MSE를 최소가 되는 지점을 찾기 위해 미분값을 이용해 값을 찾게 됩니다.
미분값을 이용한다는 것은 결국 기울기를 이용한다는 것이고, 기울기가 0이 되는 지점, 즉 Gradient 값이 0이 되는 지점을 찾는 것이 경사하강법의 기본개념이라고 할 수 있습니다.
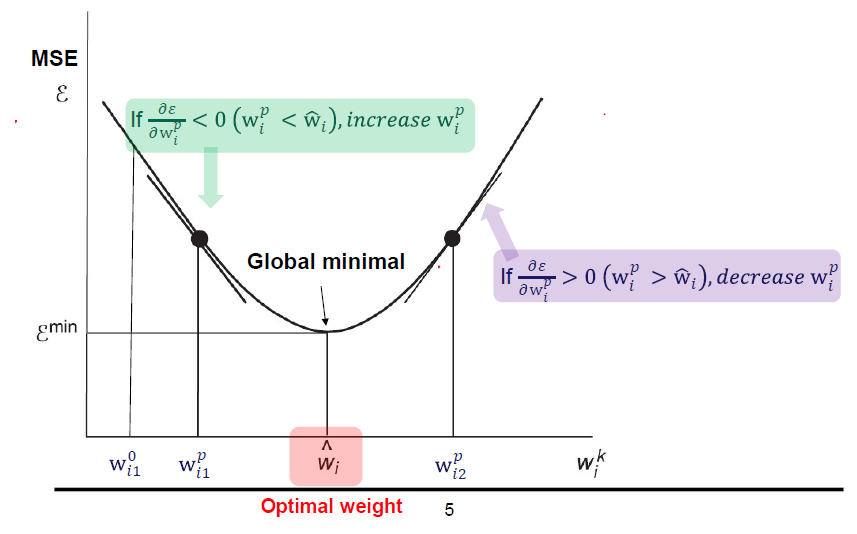

최초의 가중치는 보통 랜덤한 값으로 설정을 하는데, 초기 가중치 값이 어디냐에 따라서 최소값까지 가는데 더 빠른 경로가 될 수도 있습니다.
그리고 최초 가중치에서 이동을 하는 폭도 중요한 파라메터가 되는데 이걸 Learning Rate (학습률)이라고 합니다.

학습률이 작은값이면 보폭이 좁아지는 것이고,
학습률이 큰 값이면 보폭이 커지게 됩니다.
Learning Rate가 너무 작은 경우 최소값까지 찾아가는데 너무 오랜시간이 걸릴 수 있게되고, 너무 큰 경우에는 값을 찾아가기에 어려움이 발생합니다.
적절한 Learning Rate 설정이 중요하며 적정한 범위내에서는 Learning Rate 값을 크게하는것이 좋을 수도 있고 반대로 작게하는 것이 유리한 경우도 있습니다. (통산 0.01을 많이 사용하긴 합니다..)
결국 데이터의 특성에 따라서 Learning Rate를 조절해야 하며 Trial & Error가 필요한 경우도 있습니다.
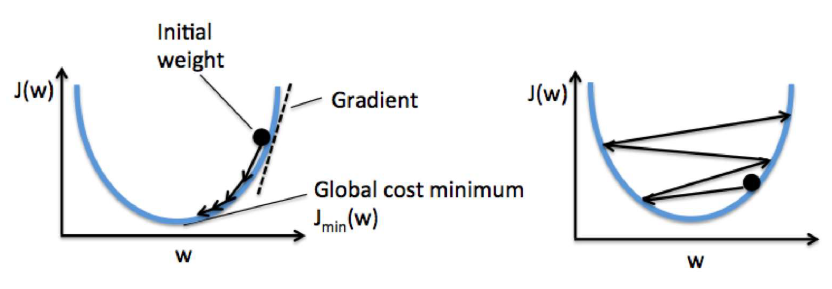
이렇게 기울기를 이용하여 손실함수의 최소값을 찾는 방법을 경사하강법, Gradient Descent라고 합니다.
Batch Gradient Descent (BGD)
Batch Grdient Descsent 에서 Batch는 데이터를 분할하는 개념이 아닌, 전체 Training 데이터셋을 의미합니다.
조금 헷갈릴수도 있는데, Gradient Descent에서 데이터를 분할하는 것은 mini-batch라는 용어를 별도로 사용하게 됩니다.
BGD는 전체 데이터셋에 대해서 에러를 구하고 기울기를 한번만 계산하는 방법입니다.


Stochastic Gradient Descent (SGD)
두번째 방법은 Stochastic Grdient Descsent 입니다.
BGD의 경우에는 전체 데이터를 모두 사용해서 기울기를 계산하기 때문에 학습하는데 많은 시간이 필요하며, 학습데이터가 큰 경우에는 학습 시간도 많이 소요되는 단점이 있습니다.
이러한 점을 보완하기 위한 방법으로 SGD를 사용하게 되는데요.

한개의 샘플을 무작위로 선택하고 해당 샘플에 대해서 기울기를 계산하게 됩니다. 매 스텝에서 한개의 샘플을 사용하기 때문에 배치 크기는 1인 되는 Gradient Descnet 방식입니다.
SGD의 경우에는 학습 속도가 빠르면 데이터셋이 크더라도 학습이 가능하다는 장점이 있습니다.

BGD와 SGD를 비교하면 위와 같이 찾아가는 방식에서 SGD의 경우에는 확률적인 노이즈가 발생하게 되면서 Loss가 좋아졌다 나빠졌다를 반복하게 되는 불안정한 모습을 보이는 특징을 갖고 있습니다.
그러나 BGD에 비해서 오히려 Local Minmum에 빠질 확률이 적고 Global Minimum을 더 잘 찾을 가능성도 높아집니다.
대부분은 BGD보다 우수한 학습능력을 가지고 있다고 볼 수 있지만 모든 데이터에 대해서 해당되는 것은 아니고 예외가 발생할 수도 있습니다.
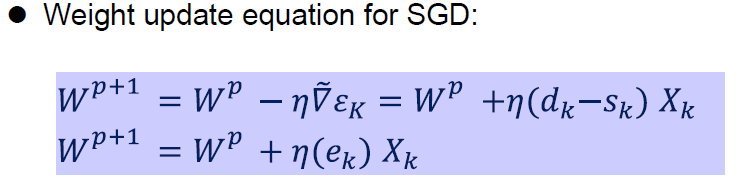
Mini-Batch Gradient Descent (MBGD)
미니배치 경사하강법은 배치 경사 하강법(BGD)이나 확률적 경사 하강법(SGD)을 혼용한 방법이라고 볼 수 있는데요.
SGD는 Batch를 1만 사용하지만, Mini Batch에서는 원하는 만큼 배치를 지정할 수 있게 되고, 전체데이터를 쓰지 않기 때문에 BGD보다는 조금 더 빠른 학습 속도를 갖습니다.

BGD, SGD, MBGD를 표현하면 위와 같이 표현할 수 있습니다.
BGD와 SGD의 개념이 서로 반대편에 있다고 한다면, MBGD는 두개의 방법을 보완한 방법이라고 할 수 있습니다.



